| Journal of Clinical Medicine Research, ISSN 1918-3003 print, 1918-3011 online, Open Access |
| Article copyright, the authors; Journal compilation copyright, J Clin Med Res and Elmer Press Inc |
| Journal website http://www.jocmr.org |
Original Article
Volume 7, Number 6, June 2015, pages 453-459
The Factor Structure of the Hospital Anxiety and Depression Scale in Orthopedic Trauma Patients
Man Hunga, b, Jerry Bounsangaa, Philip Tanga, Wei Chena, Christine Chenga
aDepartment of Orthopaedics, University of Utah, 590 Wakara Way, Salt Lake City, UT 84108, USA
bCorresponding Author: Man Hung, Department of Orthopaedics, University of Utah, 590 Wakara Way, Salt Lake City, UT 84108, USA
Manuscript accepted for publication March 16, 2015
Short title: Factor Structure of the HADS
doi: http://dx.doi.org/10.14740/jocmr2140w
| Abstract | ▴Top |
Background: Many instruments exist to assess mental disorders and anxiety, such as the hospital anxiety and depression scale (HADS). Nothing has been evaluated on the HADS factor structure for use with orthopedic trauma patients. The aim of this study was to validate the underlying structure of the HADS. Specifically, we sought to understand which of the factor structures found in the literature is appropriate for the orthopedic trauma patient population.
Methods: This study included 348 patients with an average age of 49.8 years (SD: 18.4; range: 18 - 95). Confirmatory data analysis was performed to analyze the latent structure of the HADS. Akaike information criterion (AIC) was used to compare all the models, with the lowest AIC being the best fitting model.
Results: We found that both the anxiety and the depression factors were highly correlated (with Pearson correlations greater than 0.700). After removing one item from each subscale, we found that a two-factor model was the best fitting one (AIC: 8,298.901); all other models had an AIC over 10,000.
Conclusion: Our results support a satisfactory two-factor structure for the HADS in the orthopedic trauma patients. Further studies are needed to test for higher factor structures in larger samples and in a different population.
Keywords: HADS; Depression; Anxiety; Factor analysis; Orthopedic; Trauma
| Introduction | ▴Top |
Many instruments exist to assess mental disorders and anxiety for patients. A popular instrument used is the hospital anxiety and depression scale (HADS). Zigmond and Snaith developed the HADS to assess depression and anxiety disorders among non-psychiatric patients in hospital clinics between ages 16 and 65 for both genders [1]. The HADS has two subscales: the anxiety subscale (HADS-A) and the depression subscale (HADS-D). Each subscale contains seven items for a total of 14 items in the HADS [1]. The HADS and other instruments that measure depression and anxiety can be useful when assessing patients that may be vulnerable to depression and anxiety disorders. Patients that have chronic pain and those experiencing unexpected traumatic events such as car crashes, falls, and/or accidents often report depression and anxiety. Additionally, patients experiencing chronic musculoskeletal pain are often treated for depression and anxiety [2-4]. It is crucial for clinicians that are treating patients with musculoskeletal conditions to also account for depression and anxiety [5].
Orthopedic patients are a special population as they suffer from anxiety and depression due to musculoskeletal conditions [6]. Researchers have investigated the role of the HADS in rheumatoid arthritis patients and found a high prevalence of depression and anxiety [7-10]. Additionally, depression and anxiety can negatively impact the recovery of those with musculoskeletal disorders and conditions [11, 12]. As a result, it is important to assess and study the HADS to inform physicians of possible depression and anxiety in different patient populations [13].
If the factor structure is ambiguous or unknown, clinicians may not know how to interpret the results of the assessment and may not know what intervention or treatment is appropriate for patients. For example, if we have the knowledge that the HADS instrument has two factors (e.g., depression and anxiety) and that a patient scores very high on depression, we can propose different strategies to treat this patient’s depressive symptoms. Although the HADS may be useful in determining depression and anxiety for patients, there is not a clear consensus about the factor structure of the instrument, the applicability of some of the items on the HADS for various conditions [14], and the agreement of HADS with other self-reporting instruments.
For the factor structure of the HADS, there are different opinions [14]. Depending on the medical condition being investigated, researchers have suggested one to four factors for the HADS [14, 15]. In a review of literature on the HADS, 11 of 18 studies suggested a two-factor solution [14]. Another review found that 25 of 50 studies supported a two-factor solution, five supported a one-factor solution, 17 supported a three-factor solution, and two supported a four-factor solution [15]. Others further suggested that the HADS should just be used as a one-factor general measure of distress since the study found that the symptoms of anxiety and depression were not well-separated in the HADS [16].
Research has shown that the HADS-A and HADS-D had a mean correlation of 0.56 [14]. Due to the high correlation, some scholars have suggested a single factor for calculating the total score [17, 18]. Other researchers have suggested a three-factor solution due to better fit of the data from the three factors being freely estimated [19-23]. The three-factor model includes an autonomic anxiety factor, a negative affectivity factor, and an anhedonic depression factor [20]. Researchers also raised questions about item 7 because it loaded onto two factors (negative affectivity and depression subscales). Item 7, “I can sit at ease, and feel relaxed”, an anxiety item, has demonstrated complexities in a few studies [1, 5, 14, 18]. Others have suggested the HADS should not be used in practice due to its complexities and variability of factor structure [24, 25], while some have called for additional research [26]. More recent reviews have suggested that the number of HADS factors varies widely and that the use of the HADS needs to be targeted to specific patient populations [15]. Specifically, Cosco et al [15] reported that the majority of existing research utilized factor analytic techniques from classical test theory to examine the HADS factor structure and warned that the classical test theory results would not be generalized beyond the study’s specific sample population. For results to be generalizable, item response theory methods are needed.
In reviewing the literature, we only found a single study that investigated the factor structure of the HADS for musculoskeletal patients in a rehabilitation clinic, with 55% reporting lower back pain, 20% upper or lower limb injuries, 15% cervical injuries and 10% other musculoskeletal problems. The study suggested a two-factor structure along with removing item 7, which allowed for straightforward interpretation of factors [5]. The two factors for musculoskeletal patients were interpreted as anxiety (items 1, 3, 5, 9, 11, and 13) and depression (items 2, 4, 6, 8, 10, 12, and 14). In line with the vast majority of the literature and our present study, Pallant and Bailey [5] used confirmatory factor analysis to confirm the HADS factor structure via common statistical values such as root mean square error of approximation (RMSEA) and comparative fit index (CFI). Since the patient population in our study also consisted of musculoskeletal (e.g., orthopedic) patients and our methodology was comparable to Pallant’s, we expected the factor structure for our patients to contain two factors as well. However, while Pallant et al’s patients had a wide spectrum of musculoskeletal conditions, our patients were specific to trauma. A unique study utilizing item response theory and focusing on patients with motor neuron disease [27] suggested the removal of one item from each of the two sub-scales (D8 and A11) to form two sub-scores, or the removal of three items (D8, D10 and A11) to form the 11-item high-order HADS total score. Since results from item response theory are sample independent (i.e., can be generalizable to other population), we hypothesized our results to be very close to Gibbons two-factor model.
This body of evidence from the literature suggests that the HADS factor structure is dependent on the condition and patient population [15, 28]. The sample population from previous studies primarily included adults from both genders and those having cancer, intellectual disabilities, spinal cord injury, diabetes, coronary heart disease, end-stage renal disease, schizophrenia and myotonic dystrophies. None included orthopedic trauma patients. Although all these studies essentially used factor analysis to determine the factor structure, factor analysis is a sample dependent technique from classical test theory; therefore we expected the HADS structure in the orthopedic trauma patient population to differ from what was found in studies examining populations with different medical conditions. Similar to previous studies, our population consisted of those aged at or above 18 from both genders. Despite the existence of literature on the HADS structure, there is only one study conducted in the musculoskeletal patient population and none specifically in orthopedic trauma patients. Thus, it is important to assess the HADS in the orthopedic trauma patients and to understand its internal validity. The purpose of this study was to validate the underlying structure of the HADS in orthopedic trauma patients.
| Methods | ▴Top |
We seek to understand which of the factor structures found in the literature is appropriate for the orthopedic trauma population. The following eight models, representing the most commonly found factor structures in the literature, were examined in this study. 1) Razavi: one-factor model [17]: (items 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, and 14). 2) Zigmond: two-factor model [1]: anxiety (items 1, 3, 5, 7, 9, 11, and 13); depression (items 2, 4, 6, 8, 10, 12, and 14). 3) Moorey: two-factor model [29]: anxiety (items 1, 3, 5, 7, 9, 11, and 13); depression (items 2, 4, 6, 7, 8, 10, 12, and 14). 4) Gibbons: two-factor model [27]: anxiety (items 1, 3, 5, 7, 9, and 13); depression (items 2, 4, 6, 10, 12, and 14). 5) Friedman: three-factor model [30]: psychic anxiety (items 3, 5, 9, and 13); depression (items 2, 4, 6, 8, 10, and 12); psycho-motor agitation (items 1, 7, and 11). 6) Caci: three-factor model [23]: anxiety (items 1, 3, 5, 9, and 13); depression (items 2, 4, 6, 8, 10, 12, and 14); restlessness (items 7, 11, and 14). 7) Arving: three-factor model [31]: anxiety (items 3, 5, 9, and 13); depression (items 2, 4, 6, 8, 10, and 12); restlessness (items 1, 7, 11, and 14). 8) Dunbar: three-factor model [20]: autonomic anxiety (items 3, 9, and 13); anhedonic depression (items 2, 4, 6, 8, 10, 12, and 14); negative affectivity (items 1, 5, 7, and 11).
Data
Data for this study were obtained from a university orthopedic center in the Rocky Mountain region of the US in 2014. Three hundred forty-eight orthopedic trauma patients were included in this study. Their mean age was 49.8 years (range: 18 - 95; standard deviation: 18.4; interquartile range: 35 - 64). There were 45.7% females, 88.8% Caucasians, and 6.61% Hispanics. Detailed sample characteristics were presented in Table 1. Data were collected on an iPad by receptionists at clinic check-ins as part of standard care. Institutional Review Board approval was obtained for the study.
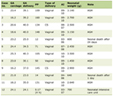 Click to view | Table 1. Sample Demographic Characteristics |
Measures
The HADS consists of 14 items (Supplementary 1, www.jocmr.org) measuring the presence of symptoms of both anxiety and depression during the past week. Each of the two subscales, anxiety and depression, has seven items, with scores ranging from 0 to 3 per item. The maximum possible score is 21 for each subscale. A score that equals to or greater than 8 on a subscale or 11 in the whole HADS was considered abnormal [1].
Statistical analysis
Descriptive statistics were performed to characterize the items and the patients. The SAS 9.4 software was used to check for missing data, normality, outliers, and data accuracy via plots and distributions. Data accuracy refers to whether the data values presented on our spreadsheet were correct or within the expected range.
Structural equation modeling, specifically confirmatory factor analyses with maximum likelihood estimation with robust standard errors, was performed to examine whether our data from the orthopedic trauma patient population were consistent with any one of the factor structures hypothesized by the literature. This approach was built on existing theoretical framework of the HADS and provided information about possible modifications of the relationship between the HADS items and factors. It was also robust to non-normality of data. To evaluate the psychometric fit of the HADS instrument, three indices were reported: the root mean square error of approximation (RMSEA), the standardized root mean square residual (SRMR), and the comparative fit index (CFI). Although utilizing one fit index is probably sufficient, it would be beneficial to use more than one in order to triangulate and confirm model specification. Therefore, three absolute fit indices (RMSEA, SRMR, and CFI) were reported in this study. They were selected because they are widely used in literature and are often reported in SEM studies [32, 33]. RMSEA is a non-centrality-based index, meaning it tests for how much misfit, rather than fit, is present in the model. Hence, the smaller the RMSEA value, the better the model fit. There were no strict guidelines as to what indicates adequate fit [34]. Since RMSEA ranges from 0 to 1, some suggest cutoff values of 0.01, 0.05, 0.08 and 0.1 as excellent, good, adequate and poor fit respectively [33, 35]. SRMR assesses the standardized difference between the observed correlation of model variables and the predicted correlation. Its values range from 0 to 1, with 0 indicating perfect fit and values less than 0.08 indicating good fit [36]. CFI is an incremental index, comparing the fit of the hypothesized model with the null model (i.e., the worst possible model in which all variables in the model are allowed to vary but are uncorrelated) [37, 38]. It penalizes for model complexity and its values range from 0 to 1, with 1 being the best fit, 0.95 being good fit, and 0.90 being adequate fit.
While RMSEA, SRMR and CFI are great for evaluating an individual model alone (e.g., testing whether model 1 specified above fits well, or testing whether model 2 specified above fits well), they are not appropriate for comparison of non-nested (e.g., different) models. That is, they cannot be used to compare whether model 1 is better than model 2 above, or vice versa. Hence, comparative measure of fit such as the Akaike information criterion (AIC) is needed to compare the eight hypothesized models in this study. A single AIC value alone is not meaningful; two or more AIC values are required for model comparison with lower values indicating better fit [39]. The model with the lowest AIC would be the best fitting model. Models with complicated structure (e.g., lack of parsimony) are often being penalized by AIC. All analyses were performed using MPlus 7.2 and SAS 9.4.
| Results | ▴Top |
HADS scores
The total HADS mean score was 10.26 (median: 8; range: 0 - 39; standard deviation: 7.71; interquartile range: 4 - 15). The mean HADS-A score was 5.26 (median: 4; range: 0 - 21; standard deviation: 4.31, interquartile range: 2 - 8). The mean HADS-D score was 5.00 (median: 4; range: 0 - 20; standard deviation: 4.08, interquartile range: 2 - 8). The Cronbach alpha reliability measures for the total HADS, the HADS-A and the HADS-D were 0.899, 0.858 and 0.822, respectively. Female had a mean HADS-A score of 5.34 and a mean HADS-D score of 5.12. Male had a mean HADS-A of 5.20 and a mean HADS-D of 4.89. There were 21.26% of patients with HADS-A of 8 or above, and 19.54% with HADS-D of 8 or above. Individual item characteristics were presented in Table 2.
 Click to view | Table 2. HADS Item Characteristics |
Confirmatory factor analysis
All factors were highly correlated (with Pearson correlations > 0.700). Note that factor correlations are only applicable for structures having two or more factors. For the one-factor model, factor correlation is not applicable as there are no other factors for the single factor to correlate with.
Fit indices for the eight models were presented in Table 3. The two-factor and three-factor models provided adequate/good fit to the data, whereas the one-factor model provided suboptimal fit (e.g., RMSEA > 0.08 and CFI < 0.90). According to RMSEA, SRMR, and CFI, model 3 (Moorey’s two-factor model) appeared to perform the best across all indices. Nonetheless, all of the models, except model 1 (Razavi one-factor model) performed adequately.
 Click to view | Table 3. Goodness of Fit Indices for the HADS Models |
Since many absolute fit indices exist (besides RMSEA, SRMR and CFI), each evaluating slightly different areas of model mis-specification, it would be difficult to do pairwise comparison of all these fit indices across the models. Additionally, these absolute fit indices are not designed for comparison of different models. In order to select the best fitting model from the two-factor and three-factor models, the AIC was examined. Model 3 showed the second lowest AIC (10,071.944). Model 4 (Gibbons two-factor model) showed the lowest AIC (8,298.901) overall and hence was considered as the best fitting model; all other models had an AIC value above 10,000.
| Discussion | ▴Top |
Our results revealed a mean total HADS score of 10.26, which is very close to the abnormal cutoff for the measure (i.e., 11). This finding is expected for patients who had recently experienced traumatic events. If we are to examine a different patient population (e.g., non-orthopedic trauma), the mean total HADS scores are likely to be lower and hence, the factor structure for HADS would probably be different. Given that the symptom level is expected to affect factor structure [15, 28], our findings for the HADS structure should be applicable to orthopedic trauma patients but not necessarily other groups.
Our study on the orthopedic trauma patient population suggested that the Gibbons’ two-factor model was the best model among all, which consists of general anxiety and depression factors. However, as suggested by Gibbons study, the standard seven-item measure of depression should be modified. Based on Gibbons work, the HADS-D subscale had a better model fitting after the removal of D8 “I feel slowed down”. Since orthopedic patients have just recently experienced a traumatic event, many may already “feel slowed down”, and this may not be a psychological disturbance but something normal as a consequence of the traumatic event. This result is also consistent with other studies on motor neuron diseases, suggesting that this item may confound the factor structure of HADS-D, at least in the orthopedic trauma patient population. Similarly, item 11 “I feel restless as if I have to be on the move” in the HADS-A subscale shows poor model fitting in Gibbons study, and indicates that a modified HADS-A subscale should be adapted to measure a patient’s anxiety status.
Considering the RMSEA, SRMR and CFI, all indicated the Moorey model to be the best fitting, it may be difficult to understand why the AIC suggested the Moorey model to be the second best while the Gibbons model is the best. Technically speaking, these two models are the same, except that the Gibbons model has excluded items 8 and 11. Since the AIC favors parsimonious model (e.g., simple model structure) and penalizes complexities (e.g., models with more parameters/items), it becomes obvious that the Gibbons model with fewer items is preferred by the AIC over the Moorey model.
Interestingly, even when all factors were highly correlated (i.e., correlations > 0.700) in the two- and three-factor models, the one-factor model was not appropriate (Table 3). These high factor correlations reflect the reality that the depression factor and the anxiety factor are related symptoms. However, they are not high enough (e.g., > 0.90) for the depression and the anxiety factors to be considered as one single factor, indistinguishable from each other.
Limitations
Although the study found that a two-factor model was the best fitting model, this may not always be the case since the HADS is dependent on conditions and patient population. Since our study only focused on orthopedic trauma patients, there may be other patient populations experiencing trauma that needs to be examined.
Conclusion
Gibbons two-factor model of the HADS is the most appropriate model for the orthopedic trauma population. Future studies that are considering the HADS as a screening tool should examine the best fitting model for other suitable patient populations. By assessing the HADS for orthopedic or different patient populations, both researchers and physicians have the opportunity to learn more about anxiety and depression, which may assist in effective treatment and further studies.
Acknowledgement
This study was supported by the Center for Outcomes Research and Assessment, the University of Utah Department of Orthopaedics, with funding in part from the National Institute of Arthritis and Musculoskeletal and Skin Diseases of the National Institutes of Health under award number U01AR067138. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
| References | ▴Top |
- Zigmond AS, Snaith RP. The hospital anxiety and depression scale. Acta Psychiatr Scand. 1983;67(6):361-370.
doi - Parker JC, Wright GE. Depression in arthritis and musculoskeletal disorders. Depression and Physical Illness Chichester: John Wiley & Sons. 1997:377-390.
pubmed - Stevens DE, Merikangas KR, Merikangas JR. Comorbidity of depression and other medical conditions. 1995.
- Linton SJ, Nicholas MK, MacDonald S, Boersma K, Bergbom S, Maher C, Refshauge K. The role of depression and catastrophizing in musculoskeletal pain. Eur J Pain. 2011;15(4):416-422.
doi pubmed - Pallant JF, Bailey CM. Assessment of the structure of the Hospital Anxiety and Depression Scale in musculoskeletal patients. Health Qual Life Outcomes. 2005;3:82.
doi pubmed - Ring D, Kadzielski J, Malhotra L, Lee SG, Jupiter JB. Psychological factors associated with idiopathic arm pain. J Bone Joint Surg Am. 2005;87(2):374-380.
doi pubmed - Covic T, Cumming SR, Pallant JF, Manolios N, Emery P, Conaghan PG, Tennant A. Depression and anxiety in patients with rheumatoid arthritis: prevalence rates based on a comparison of the Depression, Anxiety and Stress Scale (DASS) and the hospital, Anxiety and Depression Scale (HADS). BMC Psychiatry. 2012;12:6.
doi pubmed - Murphy LB, Sacks JJ, Brady TJ, Hootman JM, Chapman DP. Anxiety and depression among US adults with arthritis: prevalence and correlates. Arthritis Care Res (Hoboken). 2012;64(7):968-976.
- Geenen R, Newman S, Bossema ER, Vriezekolk JE, Boelen PA. Psychological interventions for patients with rheumatic diseases and anxiety or depression. Best Pract Res Clin Rheumatol. 2012;26(3):305-319.
doi pubmed - Traki L, Rostom S, Tahiri L, Bahiri R, Harzy T, Abouqal R, Hajjaj-Hassouni N. Responsiveness of the EuroQol EQ-5D and Hospital Anxiety and Depression Scale (HADS) in rheumatoid arthritis patients receiving tocilizumab. Clin Rheumatol. 2014;33(8):1055-1060.
doi pubmed - Cremeans-Smith JK, Contrera K, Speering L, Miller ET, Pfefferle K, Greene K, Delahanty DL. Using established predictors of post-traumatic stress to explain variations in recovery outcomes among orthopedic patients. J Health Psychol. 2013.
doi - Nota SP, Bot AG, Ring D, Kloen P. Disability and depression after orthopaedic trauma. Injury. 2015;46(2):207-212.
doi pubmed - Herrmann C. International experiences with the Hospital Anxiety and Depression Scale--a review of validation data and clinical results. J Psychosom Res. 1997;42(1):17-41.
doi - Bjelland I, Dahl AA, Haug TT, Neckelmann D. The validity of the Hospital Anxiety and Depression Scale. An updated literature review. J Psychosom Res. 2002;52(2):69-77.
doi - Cosco TD, Doyle F, Ward M, McGee H. Latent structure of the Hospital Anxiety And Depression Scale: a 10-year systematic review. J Psychosom Res. 2012;72(3):180-184.
doi pubmed - Norton S, Cosco T, Doyle F, Done J, Sacker A. The Hospital Anxiety and Depression Scale: a meta confirmatory factor analysis. J Psychosom Res. 2013;74(1):74-81.
doi pubmed - Razavi D, Delvaux N, Farvacques C, Robaye E. Screening for adjustment disorders and major depressive disorders in cancer in-patients. Br J Psychiatry. 1990;156:79-83.
doi pubmed - Martin CR, Tweed AE, Metcalfe MS. A psychometric evaluation of the Hospital Anxiety and Depression Scale in patients diagnosed with end-stage renal disease. Br J Clin Psychol. 2004;43(Pt 1):51-64.
doi pubmed - Clark LA, Watson D. Tripartite model of anxiety and depression: psychometric evidence and taxonomic implications. J Abnorm Psychol. 1991;100(3):316-336.
doi - Dunbar M, Ford G, Hunt K, Der G. A confirmatory factor analysis of the Hospital Anxiety and Depression scale: comparing empirically and theoretically derived structures. Br J Clin Psychol. 2000;39(Pt 1):79-94.
doi pubmed - Joiner T, Jr. A confirmatory factor-analytic investigation of the tripartite model of depression and anxiety in college students. Cogn Ther Res. 1996;20(5):521-39.
doi - Joiner TE, Jr., Catanzaro SJ, Laurent J. Tripartite structure of positive and negative affect, depression, and anxiety in child and adolescent psychiatric inpatients. J Abnorm Psychol. 1996;105(3):401-409.
doi pubmed - Caci H, Bayle FJ, Mattei V, Dossios C, Robert P, Boyer P. How does the Hospital and Anxiety and Depression Scale measure anxiety and depression in healthy subjects? Psychiatry Res. 2003;118(1):89-99.
doi - Coyne JC, van Sonderen E. No further research needed: abandoning the Hospital and Anxiety Depression Scale (HADS). J Psychosom Res. 2012;72(3):173-174.
doi pubmed - Coyne JC, van Sonderen E. The Hospital Anxiety and Depression Scale (HADS) is dead, but like Elvis, there will still be citings. Journal of Psychosomatic Research. 2012;73(1):77-78.
doi - Norton S, Sacker A, Done J. Further research needed: a comment on Coyne and van Sonderen's call to abandon the Hospital Anxiety and Depression Scale. J Psychosom Res. 2012;73(1):75-76; author reply 77-78.
doi pubmed - Gibbons CJ, Mills RJ, Thornton EW, Ealing J, Mitchell JD, Shaw PJ, Talbot K, et al. Rasch analysis of the hospital anxiety and depression scale (HADS) for use in motor neurone disease. Health Qual Life Outcomes. 2011;9:82.
doi pubmed - Johnston M, Pollard B, Hennessey P. Construct validation of the hospital anxiety and depression scale with clinical populations. J Psychosom Res. 2000;48(6):579-584.
doi - Moorey S, Greer S, Watson M, Gorman C, Rowden L, Tunmore R, Robertson B, et al. The factor structure and factor stability of the hospital anxiety and depression scale in patients with cancer. Br J Psychiatry. 1991;158:255-259.
doi pubmed - Friedman S, Samuelian JC, Lancrenon S, Even C, Chiarelli P. Three-dimensional structure of the Hospital Anxiety and Depression Scale in a large French primary care population suffering from major depression. Psychiatry Res. 2001;104(3):247-257.
doi - Arving C, Glimelius B, Brandberg Y. Four weeks of daily assessments of anxiety, depression and activity compared to a point assessment with the Hospital Anxiety and Depression Scale. Qual Life Res. 2008;17(1):95-104.
doi pubmed - Steiger JH. Some additional thoughts on components, factors, and factor indeterminancy. Multivariate Behavioral Research. 1990;25(1):41-45.
doi - Browne MW, Cudeck R. Alternative ways of assessing model fit. Sociological Methods & Research. 1992;21(2):230-258.
doi - Bollen KA. Structural equation models. Wiley Online Library. 1998.
- MacCallum RC, Browne MW, Sugawara HM. Power analysis and determination of sample size for covariance structure modeling. Psychological methods. 1996;1(2):130.
doi - Hu Lt, Bentler PM. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling: A Multidisciplinary Journal. 1999;6(1):1-55.
doi - Bentler PM. Comparative fit indexes in structural models. Psychol Bull. 1990;107(2):238-246.
doi pubmed - McDonald RP, Marsh HW. Choosing a multivariate model: Noncentrality and goodness of fit. Psychological Bulletin. 1990;107(2):247.
doi - Akaike H. A new look at the statistical model identification. Automatic Control, IEEE Transactions on. 1974;19(6):716-723.
doi
This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Journal of Clinical Medicine Research is published by Elmer Press Inc.


